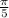Question

What is the period of the function f(x)=cos10x

Answer 1

period of the function is
`(\pi )/(5)`

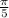
Explanation:

The given function is f (x) = cos 10x

Since cosine function is represented by

f (x) = a cos b x

where a = amplitude of cosine function and period =
`(2\pi )/(b)`

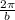
Now we compare function given with the standard form of cosine function.

we find b = 10

then period =
`(2\pi )/(b)`

=
`(2\pi )/(10)`

=
`(\pi )/(5)`

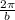
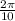
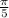
Therefore, period of the function is
`(\pi )/(5)`

Answer 2

`Period=(\pi)/(5)`

Explanation:

we are given function as

`f(x)=cos(10x)`

now, we can use formula

If
`f(x)=Acos(Bx+C)+D`

`Period=(2\pi)/(B)`

now, we can compare and find B

we get

B=10

now, we can find period

`Period=(2\pi)/(10)`

so, we get

`Period=(\pi)/(5)`