Answer:
The probability of drawing either 3 red cards or 3 face cards is: 0.1267
Explanation:
We are given a deck of 52 playing cards out of which we draw 3 cards.
We are asked to find the probability that the 3 card drawn are either 3 red cards or 3 face cards.
We know that in a playing cards we have 26 red cards and 12 face cards.
so we have to choose our card either from 26 red cards or 12 face cards and there are 6 cards which are both red card and is a face as well.
Let P denote the probability of an event.
Let A be the set that the card drawn is red.
B denote the set that the card drawn is a face card.
A∩B denote the set that the card drawn is red as well as is a face card.
We need to find the probability that the card drawn is either 3 red cards or 3 face cards i.e. we are asked to find P(A∪B)
We know that
P(A∪B)=P(A)+P(B)-P(A∩B)
Now

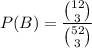
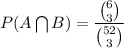
Hence,
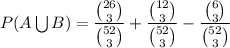
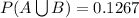
Hence, the probability of drawing either 3 red cards or 3 face cards is: 0.1267