Question

Math equation help please. 20 points!

Answer 1

(a) we are given two functions f(x) and g(x) as:

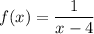`f(x)=(1)/(x-4)` and
`g(x)=(4x+1)/(x)`

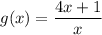
Now we find out the composition maps fog and gof as:

`fog=f(g(x))\\\\=f((4x+1)/(x))\\\\=(1)/((4x+1)/(x)-4 )\\ \\=(x)/(4x+1-4x)\\ \\=x`

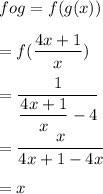
Hence,
`fog=x`

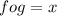
similarly we find gof.

`gof(x)=g(f(x))\\\\=g((1)/(x-4))\\\\=(4((1)/(x-4))+1 )/((1)/(x-4))\\ \\=((4+x-4)/(x-4) )/((1)/(x-4))\\ \\=x`

hence,
`gof=x`

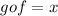
as fog=gof=x this means that f and g are inverse of each other.

(b) the domain of f is given by: (-∞,4)∪(4,∞)

since, f is defined all over the real line except at 4 ; at 4 the function is not defined as the denominator is zero.

also g is defined everywhere except at 0; since at 0 denominator is 0.

hence, domain of g(x) is (-∞,0)∪(0,∞).

domain of the composition fog is the domain of the function g(x) ( as for defining fog we need to evaluate function g(x) first and then f(g(x)) ).

and domain of function gof is equal to domain of function f(x) ( as for defining gof we need to evaluate function f(x) first and then g(f(x)) ).

hence domain of fog=(-∞,0)∪(0,∞).

and domain of gof=(-∞,4)∪(4,∞)