Answer:
The vertex of the provided equation (1,-25)
The x intercepts are (-4,0) and (6,0).
Explanation:
Consider the provided equation.
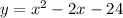
Substitute y=0 to find x intercepts.
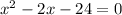
The above equation can be written as:
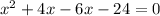
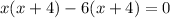
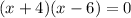
By zero product rule:If ab=0 then either a=0 or b=0
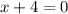 or
or
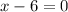
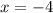 or
or
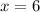
Hence, the x intercepts are (-4,0) and (6,0).
If the equation is in the standard form
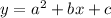 then the expression
then the expression
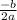 gives the x coordinate of the vertex.
gives the x coordinate of the vertex.
By comparing the provided equation with standard form we can concluded that: a=1, b=-2 and c=-24
Substitute the respective values in the expression
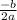 we get x coordinates of the vertex:
we get x coordinates of the vertex:
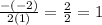
Hence, the value of x=1.
Now substitute the value of x in the provided equation to find the value of y.
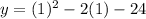
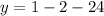
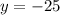
Hence, the vertex of the provided equation (1,-25)