Answer:
Monthly growth function is
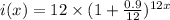 and growth rate is 0.075.
and growth rate is 0.075.
Explanation:
We are given,
The function which models the population of iguanas in a reptile garden is
 , where x is the number of years.
, where x is the number of years.
As,

i.e.
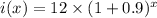
So, the monthly growth rate function becomes,

i.e.
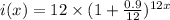 .
.
Hence, the monthly growth rate population of iguanas is i.e.
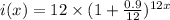 .
.
Moreover, the growth factor is
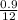 = 0.075.
= 0.075.
Hence, the growth factor rounded to nearest thousandth is 0.075