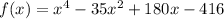Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. 4, -8, and 2 + 3i

Question

asked Jul 12, 2020 121k views

1 Answer

Sander Vanden Hautte · Answer 1 · 2020-07-18T07:45:59+0000

Answer:

Option 3

f(x) = x^4 - 35x^2+180x -416

Explanation:

To answer this question we start by writing the polynomial product form of factors:

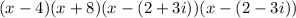
(x-4)(x + 8)(x- (2 + 3i))(x- (2-3i))

We multiply the first two factors:

$(x^2 + 8x -4x -32)(x- (2 + 3i))(x- (2-3i))\\\\(x^2 + 4x -32)(x- (2 + 3i))(x- (2-3i))$

Now we multiply the second two factors:

(x^2+ 4x -32) (x^2 -2x+ 3ix -2x -3ix + 4 - 9i^2)

We know that
i = √((-1))

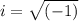
So:

i^2 = -1

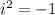
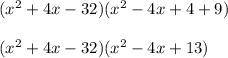
$(x^2 + 4x -32) (x^2 -4x + 4 + 9)\\\\(x^2 + 4x -32) (x^2 -4x + 13)$

Finally we multiply both terms and obtain the polynomial sought:

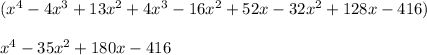
$(x^4 -4x^3 + 13x^2 + 4x^3 -16x^2 +52x-32x^2+128x -416)\\\\x^4 - 35x^2+180x -416$

Finally the correct option is the third.

f(x) = x^4 - 35x^2+180x -416