Question

Can You Please help Me

Answer 1

(a)

`(7)/(9)`

(b)

`8(1)/(3)s=37(1)/(2)`

Explanation:

(a)

we are given

w÷
`7(1)/(2)`

we have

`w=5(5)/(6) =(5* 6+5)/(6)=(35)/(6)`

w÷
`7(1)/(2)`

w÷
`(7* 2+1)/(2)=(15)/(2)`

we can also write as

=
`w* (2)/(15)`

=
`w* (2)/(15)`

now, we can plug back w

=
`(35)/(6)* (2)/(15)`

=
`(7)/(9)`

(b)

`8(1)/(3)s`

we can simplify it

`=(8* 3+1)/(3)s`

`=(25)/(3)s`

we have

`s=4(1)/(2)= (4* 2 +1)/(2)=(9)/(2)`

now, we can plug it back

and we get

`(25)/(3)s=(25)/(3)* (9)/(2)`

`(25)/(3)s=(75)/(2)`

now, we can write in mixed fraction form

`(25)/(3)s=(74+1)/(2)`

`(25)/(3)s=(37* 2+1)/(2)`

`(25)/(3)s=(37* 2)/(2)+(1)/(2)`

`(25)/(3)s=37(1)/(2)`

Answer 2

9. B.
`(7)/(9)`

10. A.
`37(1)/(2)`

Explanation:

9. We have been asked to find the quotient of expression
`w/ 7(1)/(2)` for
`w=5(5)/(6)`.

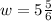Let us substitute value of w in our division problem.

`5(5)/(6)/ 7(1)/(2)`

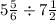
Let us convert our given mixed fractions into improper fractions.

`(35)/(6)/ (15)/(2)`

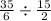
Since we know that dividing a fraction by another fraction is same as multiplying the 1st fraction by the reciprocal of the second fraction. So flipping our second fraction and multiplying by 1st fraction we will get,

`(35)/(6)* (2)/(15)`

Upon canceling out greatest common factors we will get.

`(7)/(6)* (2)/(3)`

`(7)/(3)* (1)/(3)`

`(7* 1)/(3* 3)`

`(7)/(9)`

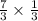
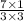
Therefore, our quotient will be
`(7)/(9)` and option B is the correct choice.

10. We are asked to find the product of
`8(1)/(3)s` for
`s=4(1)/(2)`.

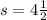Upon substituting
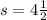`s=4(1)/(2)` in our given expression we will get,

`8(1)/(3)* 4(1)/(2)`

Let us convert our given mixed fractions into improper fractions.

`(25)/(3)* (9)/(2)`

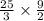
Upon canceling out greatest common factors we will get.

`(25)/(1)* (3)/(2)`

`(25* 3)/(1* 2)`

`(75)/(2)`

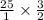
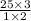
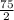
Upon converting our answer to mixed fraction we will get,

`37(1)/(2)`

Therefore, product of our given problem will be
`37(1)/(2)` and option A is the correct choice.