Answer:
0.2461
Explanation:
The binomial distribution model formula is
![P(x)=[(n!)/(x!(n-x)!)]p^(x)q^(n-x)](https://img.qammunity.org/2020/formulas/mathematics/middle-school/wrhphyderkm0id2jmcixjj3l4zg7f39iaf.png)
Where
- P(x) is the probability
- n is the is total number of questions (here n = 10)
- x is the the number of questions we are looking for (we are looking for 5 out of 10 to be right, so x = 5)
- p is the probability of success (here we want 5 questions right, so probability of being right in true of false question is
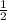 )
) - q is the probability of failure (here it means getting the answer wrong, so probability of wrong is
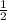 )
)
Now, we plug-in all the info into the formula and figure out the "probability that the student gets 5 out of 10 questions right":
![P(x)=[(n!)/(x!(n-x)!)]p^(x)q^(n-x)\\P(x)=[(10!)/(5!(10-5)!)]((1)/(2))^(5)((1)/(2))^(10-5)\\P(x)=[(10!)/(5!5!)]((1)/(2))^(5)((1)/(2))^(5)\\P(x)=[252]((1)/(2))^(10)\\P(x)=0.2461](https://img.qammunity.org/2020/formulas/mathematics/middle-school/l5neuyrrg8wnyf7zr2gipj3vpi9pinrgiz.png)