Answer:
-1
Explanation:
We are given that a function
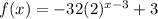
We have to find the y- intercept of the exponential function.
To find the y- intercept of given exponential we will substitute x=0
Substitute x=0 then, we get
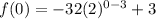
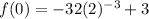
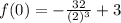
By using property
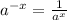
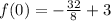
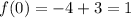
Hence, the y- intercept of given exponential =-1