Question

What is the y-intercept of the exponential function? f(x)=−32(2)x−3+3 Enter your answer in the box.

Answer 1

y-intercept for x = 0.

Substitute x = 0 to the equation of the function:

`f(x)=-32(2)^(x-3)+3\\\\f(0)=-32(2)^(0-3)+3=-32(2)^(-3)+3=-32\cdot(1)/(2^3)+3=-32\cdot(1)/(8)+3\\\\=-4+3=-1\\\\Answer:\ \boxed{y-intercept=-1\to(0,\ -1)}`

Answer 2

-1

Explanation:

We are given that a function

`f(x)=-32(2)^(x-3)+3`

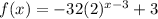
We have to find the y- intercept of the exponential function.

To find the y- intercept of given exponential we will substitute x=0

Substitute x=0 then, we get

`f(0)=-32(2)^(0-3)+3`

`f(0)=-32(2)^(-3)+3`

`f(0)=-(32)/((2)^3)+3`

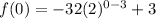
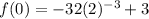
By using property
`a^(-x)=(1)/(a^x)`

`f(0)=-(32)/(8)+3`

`f(0)=-4+3=1`

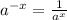
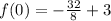
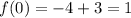
Hence, the y- intercept of given exponential =-1