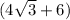Answer:
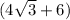
Explanation:
Simplify the radical part on by one
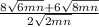
square root (6) = sqrt(3) * sqrt(2)
square root (8) =sqrt(4)* sqrt(2)= 2sqrt(2)
so given expression becomes
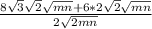
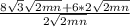
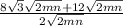
LEts factor out 2 sqrt(2mn) from the top
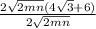
We cancel out 2sqrt(2mn) at the top and bottom