Answer:
To divide the complex number, we multiply top and bottom of the fraction by the conjugate of the denominator.
Given the complex number:
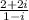
Multiply the conjugate of the denominator (1 + i) to the top and bottom.
we have;
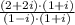
Using distributive property;
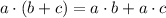
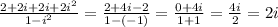 [ Since,
[ Since,
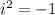 ]
]
Therefore, the standard form of this complex number
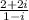 is; 0 + 2i
is; 0 + 2i