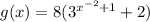Answer: The equation of g(x) is given by
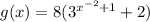
Explanation:
Since we have given that
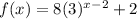
According to question, the graph of f(x) is stretched vertically by a factor of 3 to form the graph of g(x).
Equation for vertically stretch by a factor of 'a' is given by
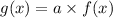
Since there is vertically stretch by a factor of 3 i.e.
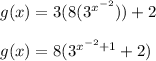
Hence, the equation of g(x) is given by