Question

An old bone contains 80% of its original carbon-14. Use the half-life model to find the age of the bone. Find an equation equivalent. How old is the bone

Answer 1

Part 1 = C. (the LAST one) /// Part 2 = 0.8 ////// Part 3 = B. (about 1,845 years)

Explanation:

theyre all correct.

Answer 2

An old bone contains 80% of its original carbon-14 in 1844.6479 years

Explanation:

We know that

half life time of C-14 is 5730 years

so, h=5730

now, we can use formula

`P(t)=P_0((1)/(2))^{(t)/(h) }`

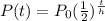
we can plug back h

and we get

`P(t)=P_0((1)/(2))^{(t)/(5730) }`

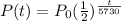
An old bone contains 80% of its original carbon-14

so,

P(t)=0.80Po

we can plug it and then we solve for t

`0.80P_0=P_0((1)/(2))^{(t)/(5730) }`

`0.80=((1)/(2))^{(t)/(5730) }`

`\ln \left(0.8\right)=\ln \left(\left((1)/(2)\right)^{(t)/(5730)}\right)`

`t=-(5730\ln \left(0.8\right))/(\ln \left(2\right))`

`t=1844.6479`

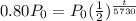
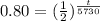
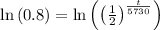
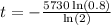
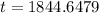
So,

An old bone contains 80% of its original carbon-14 in 1844.6479 years