Question

The first question, I don’t know how to do it.

Answer 1

see explanation

Explanation:

(a)

using the trigonometric identity

• sec x =
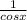`(1)/(cosx)`, then

7cos x - 3 = 2cos²x ( arrange in standard form )

2cos²x - 7cosx + 3 = 0 ← in standard form

we require the factors of the product 2 × 3 = 6 which sum to - 7

these are - 6 and - 1

use these factors to split the middle term

2cos²x - 6cosx - cosx + 3 = 0 ( factor by grouping )

2cosx(cosx - 3) - 1(cosx - 3) = 0 ( factor out (cosx - 3) )

(cosx - 3)(2cosx - 1) = 0

equate each factor to zero and solve for x

cosx - 3 = 0 ⇒ cosx = 3 ← has no solution

2cosx - 1 = 0 ⇒ cosx =
`(1)/(2)` ⇒ x = 60° , x = 300°

solution x = 60°, x = 300° for 0° < x < 360°

(b)

using the trigonometric identity

• cos2x = 1 - 2sin²x, then

1 - 2sin²x - 3sinx - 1 = 0 ← in standard form

- 2sin²x - 3sinx = 0 ( multiply through by - 1 )

2sin²x + 3sinx = 0 ( factor out sinx )

sinx(2sinx + 3) = 0

equate each factor to zero and solve for x

2sinx + 3 = 0 ⇒ sin x = -
`(3)/(2)` ← has no solution

sinx = 0 ⇒ x = 180°

solution x = 180° for 0° < x < 360°