Question

Where are the asymptotes for the following function located? (fx)-7/x^2-2x-24

Answer 1

Vertical aymptotes at x= -4 and x=6

horizontal asymptote at y=0

Explanation:

`f(x)= (-7)/(x^2-2x-24)`

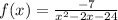
To find out vertical asymptote we take the denominator =0 and solve for x

x^2-2x-24=0

sum = -2 and product = -24

4 * (-6) = -24

4 - 6 = -2

(x+4)(x-6)=0

Now we set each factor =0 and solve for x

x+ 4=0 and x-6=0

x= -4 and x=6

Vertical aymptotes at x= -4 and x=6

Now we find horizontal asymptote

The degree of numerator is 0

degree of denominator is 2

Degree of numerator is less than the degree of denominator then horizontal asymotote is y=0

0 < 2 so horizontal asymptote at y=0