Answer:
The correct option is C.
Explanation:
The required formulas are:
1.
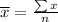
2.

3. Tread line is
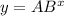
Where,
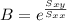 and
and
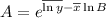
4.
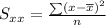
5.
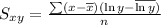
The values of x and y are
x : 0 1 2 3 4 5 6
y : 10.5 7.8 6.3 5.1 4.4 3.6 3.1
Using the above formulas,
mean of x=3
mean of
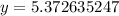
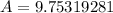

Therefore the exponential regression equation of the line is

Therefore option C is correct.