Question

Mike took out a $30,000 loan with a 7% annual interest rate. Each month he pays 2% of the balance of the loan. Which equation gives the approximate amount, A(x), he has left to pay on his loan at the end of each year as a function of x, the number of years since he took out the loan?

A(x) ≈ 30,000(0.91)x2
A(x) ≈ 30,000 + (0.785)x3
A(x) ≈ 30,000(0.840)x
A(x) ≈ 30,000(0.785)x2
A(x) ≈ 30,000(0.91)x

Answer 1

C.
`A(x)\approx 30,000(0.840)^x`

Step-by-step explanation:

We have been given that Mike took out a $30,000 loan with a 7% annual interest rate. So the approximate amount, A(x), he has to pay on his loan at the end of each year as a function of x will be:

`A(x) = 30,000((1+.07)^x*(1-0.02)^(12x))`

`A(x) = 30,000((1.07)^x*(0.98)^(12x))`

`A(x) = 30,000((1.07)^x*(0.98^(12))^x)`

`A(x) = 30,000((1.07)^x)*(0.785)^x)`

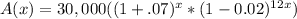
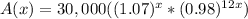
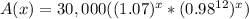
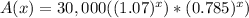
Using exponent property
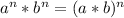`a^n*b^n=(a*b)^n` we will get,

`A(x) = 30,000(1.07*0.785)^x`

`A(x) = 30,000(0.83995)^x`

`A(x)\approx 30,000(0.840)^x`

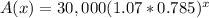
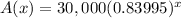
Therefore, the equation
`A(x)\approx 30,000(0.840)^x` represents the approximate amount, Mike has left to pay on his loan at the end of each year and option C is the correct choice.