Answer:
C.
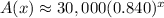
Step-by-step explanation:
We have been given that Mike took out a $30,000 loan with a 7% annual interest rate. So the approximate amount, A(x), he has to pay on his loan at the end of each year as a function of x will be:
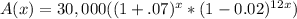
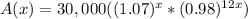
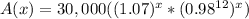
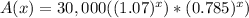
Using exponent property
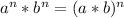 we will get,
we will get,
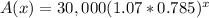
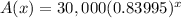
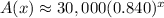
Therefore, the equation
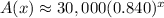 represents the approximate amount, Mike has left to pay on his loan at the end of each year and option C is the correct choice.
represents the approximate amount, Mike has left to pay on his loan at the end of each year and option C is the correct choice.