Question

a population is known to have a standard deviation of 26.1. A sample space of 35 items has a mean of 562. construct a 90% confidence interval estimate of the mean of the population. a. 566<μ<558 b. 555<μ<569 c.551<μ<573 d.561<μ<563

Answer 1

The correct option is B.

Explanation:

The value of μ is

`\mu=\overline{X}\pm z* (\sigma)/(√(n))`

Where,
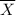`\overline{X}` is sample mean of the data, z represents the z-score, σ is standard deviation, and n is numbers of samples.

The standard deviation of the sample is 26.1. A sample space of 35 items has a mean of 562. construct a 90% confidence interval estimate of the mean of the population.

From the z-table the value of z at 90% confidence interval with 34 degree of freedom is 1.691.

`\mu=562\pm 1.691* (26.1)/(√(35))`

`\mu=562\pm 1.691* 4.41170521`

`\mu=562\pm 7.46`

`\mu=562\pm 7.46`

`554.54<\mu<569.46`

`555<\mu<569`

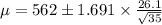
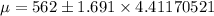
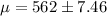
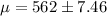
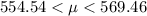
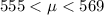
Therefore option B is correct.