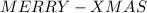Question

It’s a precalculus holiday equation. Need to simplify to find the “secret message” can anyone help???

Answer 1

Take the expression in chunks:

>>

`((X+A)(X-A)M+A^2M)E=((X^2-A^2)M+A^2M)E=X^2ME`

>>

`\frac{\frac{R+X}X+\frac X{R-X}}{\frac X{R-X}}=\frac{\frac{R+X}X}{\frac X{R-X}}+1`

`(((R+X)(R-X))/(X(R-X)))/((X^2)/(X(R-X)))=((R+X)(R-X))/(X^2)=(R^2-X^2)/(X^2)=(R^2)/(X^2)-1`

`\implies\frac{\frac{R+X}X+\frac X{R-X}}{\frac X{R-X}}=(R^2)/(X^2)`

>>

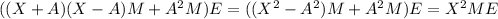
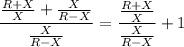
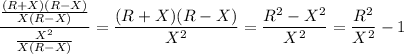
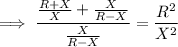
Note that
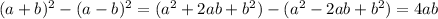`(a+b)^2-(a-b)^2=(a^2+2ab+b^2)-(a^2-2ab+b^2)=4ab`. So

`\displaystyle\frac{4AS}3\sum_(\rm cyc)\frac1{X((E+Y)^2-(E-Y)^2)}=\frac{4AS}3\sum_(\rm cyc)\frac1{4XEY}=\frac{AS}3\sum_(\rm cyc)\frac1{XEY}`

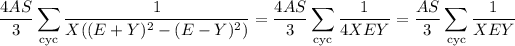
where the cyclic sum notation means

`\displaystyle\sum_(\rm cyc)f(x,y,z)=f(x,y,z)+f(z,x,y)+f (y,z,x)`

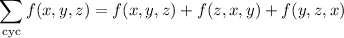
In other words, we take the sum over all possible cycles of the sequence of arguments to the summand. The second square-bracketed chunk reduces to

`\displaystyle\frac{AS}3\sum_(\rm cyc)\frac1{XEY}=\frac{AS}3\left(\frac1{XEY}+\frac1{EYX}+\frac1{YXE}\right)=\frac{AS}3\frac3{XEY}=(AS)/(XEY)`

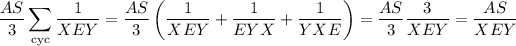
So to recap, we've reduced the starting expression to

`X^2ME\left((R^2)/(X^2)-(AS)/(XEY)\right)Y`

>>

`(R^2)/(X^2)-(AS)/(XEY)=(R^2EY-ASX)/(X^2EY)`

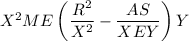
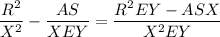
Finally, we have

`X^2ME(R^2EY-ASX)/(X^2EY)Y=M(R^2EY-ASX)`

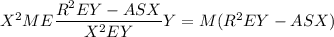
Then distributing
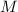`M` and rewriting to decode the message, we have

`MERRY-XMAS`