Answer:
only one number c=0 in the interval [-1,1]
Explanation:
Given : Function
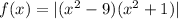 in the interval [-1,1]
in the interval [-1,1]
To find : How many numbers in the interval [−1, 1] satisfy the conclusion of the mean value theorem.
Mean value theorem : If f is a continuous function on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point 'c' in (a,b) such that
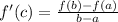
Solution : f(x) is a function that satisfies all of the following :
1) f(x) is continuous on the closed interval [-1,1]

2) f(x) is differentiable on the open interval (-1,1)
Then there is a number c such that
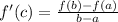
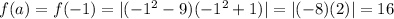
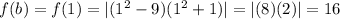
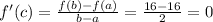
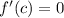 ........[1]
........[1]
Now, we find f'(x)
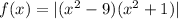
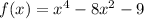
Differentiating w.r.t x
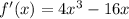
In place of x we put x=c
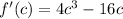
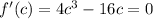 (by [1], f'(c)=0)
(by [1], f'(c)=0)
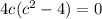

either c=0 or
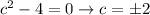
we cannot take
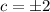 because they don't lie in the interval [-1,1]
because they don't lie in the interval [-1,1]
Therefore, there is only one number c=0 which lie in interval [-1,1] and satisfying the conclusion of the mean value theorem.