Question

If f(x) = |(x2 − 9)(x2 + 1)|, how many numbers in the interval [−1, 1] satisfy the conclusion of the mean value theorem?

Answer 1

only one number c=0 in the interval [-1,1]

Explanation:

Given : Function
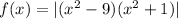`f(x) = |(x^2-9)(x^2 + 1)|` in the interval [-1,1]

To find : How many numbers in the interval [−1, 1] satisfy the conclusion of the mean value theorem.

Mean value theorem : If f is a continuous function on the closed interval [a,b] and differentiable on the open interval (a,b), then there exists a point 'c' in (a,b) such that
`f'(c)=(f(b)-f(a))/(b-a)`

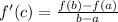
Solution : f(x) is a function that satisfies all of the following :

1) f(x) is continuous on the closed interval [-1,1]

`\lim_(x\to a) f(x)=f(a)`

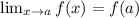
2) f(x) is differentiable on the open interval (-1,1)

Then there is a number c such that
`f'(c)=(f(b)-f(a))/(b-a)`

`f(a)=f(-1) = |(-1^2-9)(-1^2 + 1)|=|(-8)(2)|=16`

`f(b)=f(1) = |(1^2-9)(1^2 + 1)|=|(8)(2)|=16`

`f'(c)=(f(b)-f(a))/(b-a)=(16-16)/(2)=0`

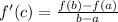
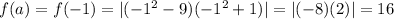
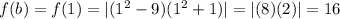
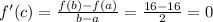
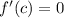`f'(c)=0` ........[1]

Now, we find f'(x)

`f(x) = |(x^2-9)(x^2 + 1)|`

`f(x) =x^4-8x^2-9`

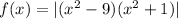
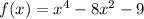
Differentiating w.r.t x

`f'(x) =4x^3-16x`

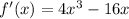
In place of x we put x=c

`f'(c) =4c^3-16c`

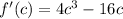
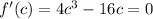`f'(c) =4c^3-16c=0` (by [1], f'(c)=0)

`4c(c^2-4)=0`

`4c=0,c^2-4=0`

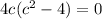
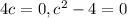
either c=0 or
`c^2-4=0\rightarrow c=\pm2`

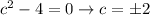
we cannot take
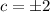`c=\pm2` because they don't lie in the interval [-1,1]

Therefore, there is only one number c=0 which lie in interval [-1,1] and satisfying the conclusion of the mean value theorem.