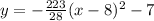Question

What is the equation of the quadratic graph with a focus of (8, −8) and a directrix of y = −6?

A) f(x) = −one fourth (x − 7)2 + 1
B) f(x) = −one fourth (x − 8)2
C) f(x) = −one fourth (x − 8)2 − 7
D) f(x) = one fourth (x − 7)2

Answer 1

The answer is C

Answer 2

`y=-(223)/(28)(x-8)^2-7`

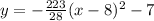
Explanation:

we are given a quadratic equation

we know that quadratic equation is same as equation of parabola

so, we can use formula

`y=a(x-h)^2+k`

Focus is

`(h,k+(1)/(4a) )`

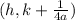
now, we can compare it with given focus

=(8,-8)

we get

`h=8`

`k+(1)/(4a)=-8`

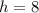
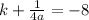
Directrix is

`y=k-(1)/(4a)`

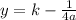
we are given directrix =-6

`k-(1)/(4a)=-6`

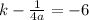
we got two equations as

`k+(1)/(4a)=-8`

`k-(1)/(4a)=-6`

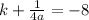
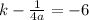
now, we can add both equations

and we get

`k+(1)/(4a)+k-(1)/(4a)=-8-6`

`2k=-8-6`

`2k=-14`

`k=-7`

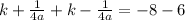
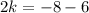
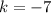
now, we can find 'a'

`k+(1)/(4* -7)=-8`

`k=-(223)/(28)`

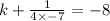
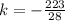
now, we can plug back all values

and we get

So, equation of parabola is

`y=-(223)/(28)(x-8)^2-7`