Find the volume of the solid formed by rotating the region bounded by the graph of y equals 1 plus the square root of x, the y-axis, and the line y = 3 about the line y = 5.

Question

asked Aug 7, 2020 73.5k views

1 Answer

Miette · Answer 1 · 2020-08-13T16:51:26+0000

Answer:

Volume of solid is
$(40)/(3)\pi$

Explanation:

We need to find the volume of solid formed by rotating the region bounded by the graph of
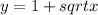y=1+sqrt{x} , y-axis and the line y=3 about the line y=5.

Please see the attachment for figure.

Using Shell method,
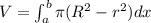
$V=\int_a^b\pi (R^2-r^2)dx$

where,

a=0 (Lower limit of solid)

b=4 (Upper limit of solid)

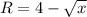R=4-√(x) (Outer Radius of Shell)

r=2 (Inner radius of shell)

dx is thickness of shell

Volume of shell, dV=Area of shell x Thickness

Volume of solid
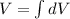
$V=\int dV$

$V=\int_0^4 \pi [(4-√(x))^2-2^2]dx$

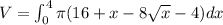
$V=\int_0^4 \pi (16+x-8√(x)-4)dx$

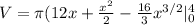
$V=\pi (12x+(x^2)/(2)-(16)/(3)x^(3/2)|_0^4$

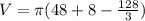
$V=\pi (48+8-(128)/(3))$

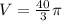
$V=(40)/(3)\pi$

Thus, Volume of solid is
$(40)/(3)\pi$