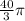Answer:
Volume of solid is
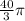
Explanation:
We need to find the volume of solid formed by rotating the region bounded by the graph of
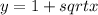 , y-axis and the line y=3 about the line y=5.
, y-axis and the line y=3 about the line y=5.
Please see the attachment for figure.
Using Shell method,
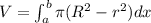
where,
a=0 (Lower limit of solid)
b=4 (Upper limit of solid)
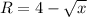 (Outer Radius of Shell)
(Outer Radius of Shell)
r=2 (Inner radius of shell)
dx is thickness of shell
Volume of shell, dV=Area of shell x Thickness
Volume of solid
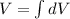
![V=\int_0^4 \pi [(4-√(x))^2-2^2]dx](https://img.qammunity.org/2020/formulas/mathematics/high-school/b68spf3zcv3eehmeikx4udlqr50lit48qn.png)
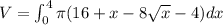
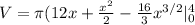
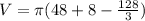
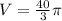
Thus, Volume of solid is