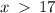ANSWER
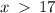
Step-by-step explanation
The given function is
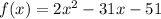
Let us split the middle term to get,

We factor to obtain,
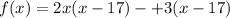

Let us find the zeros of f(x),
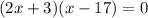
Either
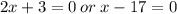

We need to find the x-value of the vertex, which is the midpoint of the x-intercepts.
This gives us,
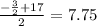
Hence the axis of symmetry of the parabola has equation,

Since the given function has minimum turning point, it will decrease and then increase.
The function will be increasing for
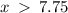
The function will be increasing and positive for