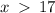Question

For the function F(x) = 2x^2-31x-51, where is the function increasing and positive? ( for all X values greater than what number )

Answer 1

ANSWER

`x \: > \: 17`

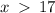
Step-by-step explanation

The given function is


`f(x) = 2 {x}^(2) - 31x - 51`
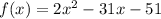
Let us split the middle term to get,


`f(x) = 2 {x}^(2) -34x + 3x- 51`

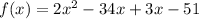
We factor to obtain,


`f(x) = 2x(x - 17) -+3(x - 17)`


`f(x) = (2x -+3)(x -17)`

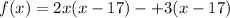
Let us find the zeros of f(x),


`(2x +3)(x - 17) = 0`

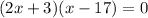
Either


`2x +3 = 0 \: or \: x - 17 = 0`

`x = -(3)/(2) \: or \: x = 17`

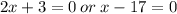
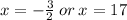
We need to find the x-value of the vertex, which is the midpoint of the x-intercepts.

This gives us,


`(- (3)/(2) + 17)/(2) = 7.75`
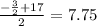
Hence the axis of symmetry of the parabola has equation,


`x = 7.75`

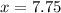
Since the given function has minimum turning point, it will decrease and then increase.

The function will be increasing for

`x \: > \: 7.75`

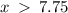
The function will be increasing and positive for

`x \: > \: 17`