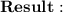A linear function contains these points: (0,-1) & (3,8) What is the slope and y-intercept of this function?

Question

asked Feb 10, 2023 22.4k views

2 Answers

Athom · Answer 1 · 2023-02-12T19:14:07+0000

$\Large\maltese\underline{\textsf{A. What is Asked}}$

If a linear function contains these points: (0,-1) and (3,8), what is its slope and y-int.?

$\Large\maltese\underline{\textsf{B. This problem has been solved!}}$

Formula utilised, here
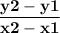$\bf{(y2-y1)/(x2-x1)}$ .

Put in the values,

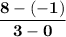$\bf{(8-(-1))/(3-0)}$ | subtract on top and bottom

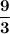$\bf{(9)/(3)}$ | divide on top and bottom

$\bf{3}$

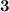
The y-intercept is the second co-ordinate of the point (0,-1)

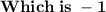$\bf{Which\;is\;-1}$ .

$\cline{1-2}$

$\bf{Result:}$

$\bf{\begin{cases} \bf{Slope=3} \\ \bf{Y-int. -1} \end{cases}$

$\LARGE\boxed{\bf{aesthetic\\ot1 \theta l}}$

Arilwan · Answer 2 · 2023-02-15T14:23:04+0000

Answer:

slope: 3

y-intercept: (0, -1)

Find slope:

$\sf slope : (y_2 - y_1)/(x_2- x_1) = (\triangle y)/(\triangle x) \ \ \ where \ (x_1 , \ y_1), ( x_2 , \ y_2) \ are \ points$

Here given points are: (0, -1), (3, 8)

$\rightarrow \sf slope : (8-(-1))/(3-0) = (9)/(3) = 3$

When finding y-intercept, the value of x is 0. Here given y is -1 when x is 0.

y-intercept: -1 or (0, -1)