Question

A supplier sells 2 1/4 pounds of mulch for every 1 1/3 pounds of gravel. The supplier sells 1/72 pounds of mulch and gravel combined. How many pounds of each item does the supplier sell?

Answer 1

108 pounds of mulch.

64 pounds of gravel.

Explanation:

Let x be the amount of mulch sold and y be the amount of gravel sold.

We have been given that a supplier sells 2 1/4 pounds of mulch for every 1 1/3 pounds of gravel.

`2(1)/(4)=(9)/(4)`

`1(1)/(3)=(4)/(3)`

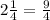
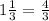
We can represent this information as:

`(x)/(y)=((9)/(4))/((4)/(3))...(1)`

We are also told that the supplier sells 172 pounds of mulch and gravel combined. We can represent this information as:

`x+y=172...(2)`

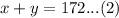
From equation (1) we will get,

`(x)/(y)=(9)/(4)*(3)/(4)`

`(x)/(y)=(27)/(16)`

`x=y*(27)/(16)`

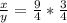
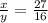
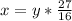
Substituting this value in equation (2) we will get,

`y*(27)/(16)+y=172`

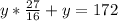
Now let us have a common denominator.

`(27y)/(16)+(16y)/(16)=172`

`(27y+16y)/(16)=172`

`16*(43y)/(16)=16*172`

`43y=2752`

`y=(2752)/(43)`

`y=64`

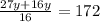
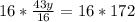
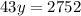
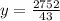
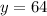
Therefore, the supplier sold 64 pounds of gravel.

Upon substituting y=64 in equation (2) we will get,

`x+64=172`

`x=172-64`

`x=108`

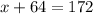
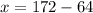
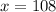
Therefore, the supplier sold 108 pounds of mulch.