Final Answer:
when ( a = 6 ), ( b = 81 ), indicating the direct proportionality between the squares of the values of ( a ) and ( b ).
Step-by-step explanation:
Direct proportionality between
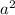 and \( b \) means that when ( a ) increases by a certain factor, ( b ) will also increase by the square of that factor. Initially, \( a = 2 \) when ( b = 9 ). Therefore, the ratio of ( a ) to ( b ) is ( 2^2 : 9 = 4 : 9 ). To find ( b ) when ( a = 6 ), use this ratio.
and \( b \) means that when ( a ) increases by a certain factor, ( b ) will also increase by the square of that factor. Initially, \( a = 2 \) when ( b = 9 ). Therefore, the ratio of ( a ) to ( b ) is ( 2^2 : 9 = 4 : 9 ). To find ( b ) when ( a = 6 ), use this ratio.
Calculate the ratio between ( a ) and ( b ) at ( a = 6 ):
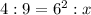
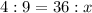
Cross multiply to find ( x ):
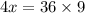
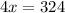
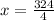
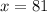
Therefore, when ( a = 6 ), ( b = 81 ), indicating the direct proportionality between the squares of the values of ( a ) and ( b ).