Question

The two lines y=6x+15 and y=mx-4 intersect at x=-2 what is the y-coordinate of their intersection point? What is the value of m?

Answer 1

y= 3

m= -7/2

Explanation:

To find the y coordinate substitute the x variable in the equation y=6x+15 for -2 (the x value). It should look like y=6(-2)+15. Solve and you will end up with y=3

To find the slope (m) substitute the y and x variables for the values you found (-2 and 3). The equation will look like this: 3= -2m-4. Solve and you will be left with m= -7/2.

I hope this helps and good luck with your math!

Answer 2

y=3 and m=
`-(7)/(2)`.

Explanation:

We are given two lines y=6x+15 and y=mx-4.

x-coordinate of the intersection point is x=-2.

In order to find the y-coordinate of intersection point, we need to plug x=-2 in first equation.

Plugging x=-2 in y=6x+15, we get

y=6(-2)+15

y=-12+15

y=3.

Therefore, y-coordinate of the intersection point is y=3.

Now, in order to find the value of m, we need to plug x and y-coordinate values in second equation and solve for m.

Plugging x=-2 and y=3 in second equation y=mx-4, we get

3=m(-2)-4

3 = -2m -4

Adding 4 on both sides, we get

3+4=-2m-4+4

7=-2m.

Dividing both sides by -2, we get.

`(7)/(-2) =(-2m)/(-2)`

`-(7)/(2)=m`

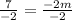
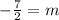
Therefore, m=
`-(7)/(2)`.