Question

Suppose a 0.04-kg car traveling at 2.00 m/s can barely break an egg. What is the min

imum speed a 0.08-kg car would need to have in order to break the egg?


A. 1.42 m/s
B. 1.00 m/s
C. 0.80 m/s
D. 2.00 m/s

Answer 1

Answer: A1.42m/s

Explanation: The kinetic energy of the car determines whether it will break the egg. The 0.04-kg car has a kinetic energy of 0.5 • 0.04 • 2.002 = 0.08 J, so assume this is the minimum energy needed to break the egg. A 0.08-kg car traveling at 1.42 m/s has a kinetic energy of 0.5 • 0.08 • 1.422 = 0.081 J,, which is just over the minimum energy required.

Answer 2

Answer: The correct answer is option (A).

Step-by-step explanation:

Momentum of the car with 0.04 kg mass , which travelling with velocity of 2.00 m/s

`P_1=mass* velocity=m_1* v_1=0.04 kg* 2.00 m/s=8.00 kg m/s`

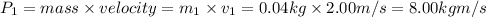
Then the maximum speed of the another car in order to not to break the eggs will be same as first car:

`P_1=P_2`

`0.08 kg m/s=m_2* v_2=0.08 kg* v_2`

`v_2=1 m/s`

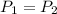
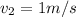
Speed slightly more than 1 m/s will increase the momentum of second car and the eggs will break. So, from the given options the minimum speed need by the second car will be 1.42m/s.