Answer: The correct answer is option (A).
Step-by-step explanation:
Momentum of the car with 0.04 kg mass , which travelling with velocity of 2.00 m/s
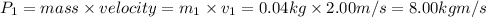
Then the maximum speed of the another car in order to not to break the eggs will be same as first car:
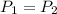

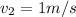
Speed slightly more than 1 m/s will increase the momentum of second car and the eggs will break. So, from the given options the minimum speed need by the second car will be 1.42m/s.