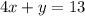Question

What is the equation of a line ,in standard form that passes through (4, -3) and is parallel to the line whose equations is 4x+y-2=0

4x-y=13
4x+y=13
4x+y=-13

Answer 1

4x + y = 13

Explanation:

1. Change 4x + y -2=0 into slope intercept form to find the slope:

y = -4x +2 The slope is -4

2. Plug in x, y and m into y = mx + b

-3 = -4 (4) + b

-3 = -16 + b

13 + b

3. Plug m and b into equation y = mx + b

y = -4x + 13

4. Change equation into standard form:

4x - y = 13

Answer 2

The equation of the parallel line to the line given is
`4x+y=13`

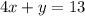
Explanation:

First you should find the slope of the line, as two parallel lines have the same slope, so if you know the slope of the first one then you know the slope of its parallel line, then you should use the point to write the equation of the parallel line.

1. Write the equation of the line given in the form
`y=mx+b` where m is the slope:

`4x+y-2=0\\4x+y=2\\y=-4x+2`

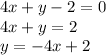
so, the slope of the line an its parallel is -4.

2. Replace the given point (4,3) in the point-slope equation
`y-y_(1)=m(x-x_(1))`:

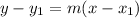Let´s name:

`x_(1)=4`

`y_(1)=-3`

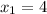
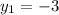
Then replace the point values and the slope on the point-slope equation:

`y-(-3)=-4(x-4)\\y+3=-4(x-4)\\y+3=-4x+16\\4x+y=16-3\\4x+y=13`

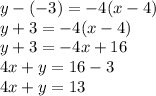
Therefore the equation of the parallel line to the line given is
`4x+y=13`