Question

Find the sum of the first six terms in the sequence {1, 5, 9, 13, …}

Answer 1

`\text{First let's find two more terms, because we have only six. We can do that by}\\\text{adding 4:: 13+4=17; 17+4=21}`

`\rule{300}{1.7}`

`\text{Now we just add the terms: 1+5+9+13+17+21}`

`\rule{300}{1.7}\\\text{66}`

Answer 2

66

Explanation:

The sequence you provided seems to be arithmetic as it increases as 4 each term. Assuming 1 is the first term the equation would be
`a_(n)=1 + 4(n-1)`. You could just take the first 6 terms and add them together since you already have 4 values calculated and you could calculate the other 2 by adding 4. This would give you

(1 + 5 + 9 + 13 + 17 + 21) = 66

But there's an easier way to do it. You could use the formula
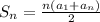`S_n = (n(a_1 + a_n))/(2)`. You can calculate
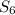`S_6` by plugging in those values. You would need to calculate
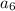`a_6` before hand, but you can calculate that using the formula I defined above. Which in general is
`a_n = a_1 + d(n-1)` where d is like the slope, or how much it changes each term. So if you calculate
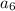`a_6` you'll get
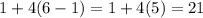`1+4(6-1) = 1+4(5) = 21`. Now plug this into the series formula above and you get
`S_6 = (6(1+21))/(2)=(6(22))/(2)=(132)/(2)=66` which is exactly what you get if you add the first 6 terms as shown above when you do it manually.