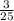Answer:
The probability of drawing two green marbles without replacement is
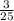
Explanation:
We are given the following information in the question:
Number of blue marbles = 6
Number of red marbles = 10
Number of green marbles = 9
Total number of marbles = 25
Formula:
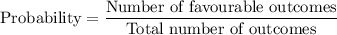

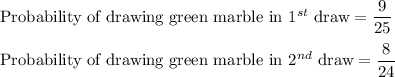
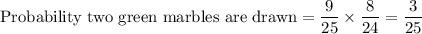
Hence, the probability of drawing two green marbles without replacement is