Four positive numbers form a geometric sequence. The sum of the four numbers is one more then the common ratio. If the first number is 1/10, find the common ratio.

Question

asked Nov 15, 2020 37.2k views

1 Answer

Emson · Answer 1 · 2020-11-21T10:40:51+0000

Answer:

r=3 where r is the common ratio

Explanation:

The sum of geometric progression for n terms is given by:

S_(n)=a_(1) ( 1-r^(n))/ 1-r , where
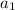a_(1) is the

first term of the series and r is the common ratio.

Now, according to the question, there are four terms and they form a geometric progression. So sum of four terms is given as
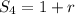and
.

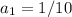Also according to the above formula:

S_(4)=a_(1) ( 1-r^(4))/ 1-r

Using the values as given in the question into the above equation we get:

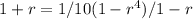
1+r =1/10 ( 1-r^(4))/ 1-r

(1+r)(1-r)=1/10 ( 1-r^(4))

[ Using formula
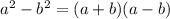a^(2) -b^(2) =( a+b)(a-b) ]

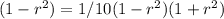
(1-r^(2))=1/10 ( 1-r^(2))(1+r^(2))

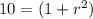
10=(1+r^(2))

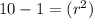
10-1=(r^(2))

√(9)=(r)

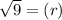
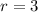which is the required answer.