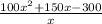Part A: What does the numerator of this rational expression represent?
ANSWER:
Numerator (200x-300) gives profit when x watches are sold.
------
Part B: What does the denominator of this rational expression represent?
ANSWER:
Denominator (x) represents the number of watches sold.
------
Part C: Rewrite the expression
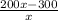
as a sum of two fractions, and simplify.
ANSWER:
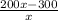
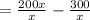
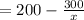
Hence simplified fraction form is
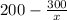
------
Part D: What does each part in the expression from part C represent?
ANSWER:
First part is (200) which means maximum average prfit can be 200.
Second part
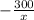
is negative and number of watches (x) is in denominator so as the number of sold watches increases, then
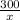
decreases and due to negative sign, decrease in average profit value becomes less.
------
Part E: Ryan also earns money by selling colored watch bands with the watches he sells. The linear expression 100x – 50 models Ryan’s additional income. What is the expression that models the new average profit, including the bands? Note: To obtain the new average profit expression, add the linear expression to the original rational expression. Write the new profit expression as one fraction.
ANSWER:
We just need to add both profit expressions:

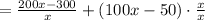
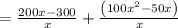
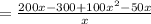

Hence final profit expression is