Answer:
Values of a and b are;
a = -8 and b = -29
Explanation:
As per the statement:
Difference of two numbers, a and b is 21
i.e, a -b = 21 .......[1]
Also, it is given that the difference of five times a and two times b is 18.
"five times a" means 5a
"two times b" means 2b
then;
5a - 2b = 18 ......[2]
We can write equation [1] as;
a = b + 21 .....[3]
Substitute the value of a in equation [2] we have;
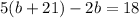
Using distributive property;

5b + 105 - 2b = 18
combine like terms we get;
3b = 18 -105
Simplify:
3b = -87
Divide by 3 on both sides we get;
b = -29
Substitute the value of b in equation [3] to solve for a;
a = -29 + 21 = -8
Therefore, the values of a and b is, -8 and -29