Answer:
We are given the profit function
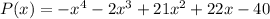 , where x is the number of commercials aired in 24- hour period.
, where x is the number of commercials aired in 24- hour period.
Now, as
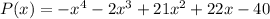 .
.
Using long division gives us that this polynomial can be factorized as,
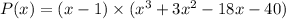
i.e.
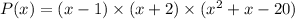
i.e.
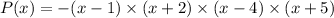 .
.
Since we want to find where will the company break.
So, we equate P(x) = 0.
i.e.
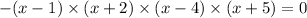 .
.
i.e. (x-1) = 0, (x+2) = 0, (x-4) = 0 and (x+5) = 0.
i.e. x = 1, x = -2, x = 4 and x = -5.
Since, x represents the number of commercials. Therefore, it cannot have negative values.
Thus, x = 1 and x = 4.
This implies that the company will break even the number of commercials is 1 and 4.
Graphically, as the degree of the polynomial is 4 .i.e even and the leading co-efficient is -1 i.e. negative, this gives us that the function P(x) will increase at the start and will decrease in the end.
Moreover, we can see from the graph below that,
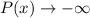 as
as
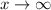 and
and
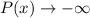 as
as
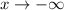 .
.
Hence, the company will face huge loss as the number of commercials increases without any bounds.
Further, as the value of x is always positive i.e.x ≥ 0. The y-intercept is when x = 0 i.e. P(0) = -40 i.e. y-intercept is at ( 0,-40 ).
Also, we can see that since the roots of P(x) are not repeating, P(x) cuts x-axis at 4 points namely (-5,0), (-2,0), (1,0) and (4,0).