Question

Solve the problems below. Please answer with completely simplified exact value(s) or expression(s). Given: ΔАВС, m∠ACB = 90 CD ⊥ AB , m∠ACD = 30°,AD = 8 cm. Find: Perimeter of ΔABC

Answer 1

Perimeter is 75.7128129211 units

Explanation:

Given ΔАВС, m∠ACB = 90°, CD ⊥ AB and m∠ACD = 30, AD = 8 cm

we have to find the perimeter of ΔABC

In triangle ADC,

`\sin 30^(\circ)=(AD)/(AC)=(8)/(AC)`

`(1)/(2)=(8)/(AC)` ⇒
`AC=16units`

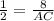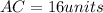
and also,
`\tan 30^(\circ)=(AD)/(CD)=(8)/(CD)`

`(1)/(√(3))=(8)/(CD)` ⇒
`CD=8√(3)units`

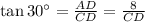
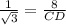Now, in triangle BDC,

∠BDC + ∠ADC = 180°

∠BDC = 180°- 90° = 90°

and also ∠DCB=∠ACB - ∠ACD = 90° - 30° = 60°

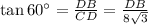
`\tan 60^(\circ)=(DB)/(CD)=(DB)/(8√(3) )`

DB=
`{√(3)}*{8}{√(3)}` ⇒
`DB=24units`

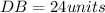
and also
`\sin 60^(\circ)=(DB)/(BC)=(24)/(BC)`

`(√(3))/(2)=(24)/(BC)` ⇒
`BC=(48)/(√(3)) units`

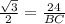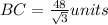
Hence, Perimeter = AC+AD+DB+BC

= 16+8+24+
`(48)/(√(3) )`

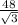
= 75.7128129211 units