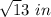Question

Solve the problems below. Please answer with completely simplified exact value(s) or expression(s). Chapter Reference c In ΔABC, AC = BC, CD ⊥ AB with D ∈ AB , AB = 4 in, and CD = 3 in. Find AC.

Answer 1

Based on the given information, the length of AC in triangle ABC is
`\sqrt13\ in`

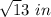
How to calculate the length of the segment

In triangle ABC, AC = BC, CD is perpendicular to AB with D lying on AB, AB = 4 in, and CD = 3 in.

Given AC = BC in an isosceles triangle, the altitude CD divides the base AB into two equal segments.

So, AD = BD = AB/2 = 4/2 = 2 in.

Using the Pythagorean theorem in right triangle ACD:

`AC^2 = AD^2 + CD^2\\AC^2 = 2^2 + 3^2\\AC^2 = 4 + 9\\AC^2 = 13`

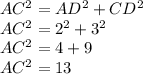
Therefore:

AC =
`\sqrt13\ in`

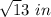
Hence, the length of AC in triangle ABC is
`\sqrt13\ in`

Answer 2

AC = √13 in

Explanation:

CD is the altitude of isosceles triangle ABC, so D is the midpoint of AB, and AD = 2.

AD and CD are the legs of right triangle ACD, so ...

AC² = CD² + AD² = (3 in)² + (2 in)² = (9 +4) in² = 13 in²

AC = √(AC²) = √13 in ≈ 3.6055 in