Answer:
13.
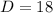
14.
Explanation:
13.
Given
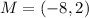
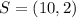
Required
Determine the distance between M and S
Distance (D) is calculated using:
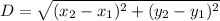
Where
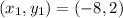
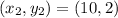
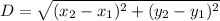
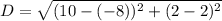
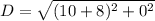
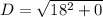
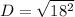
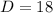
Hence, the distance between M and S is 18 units
14.
The coordinate of S and P are not given,
So, I'll just use (x,y) for P
i.e.
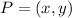
Required
Determine the coordinates of S
If S is 6 units above P, then the coordinates of S is
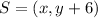
i.e. we add the units to the y coordinate of P.