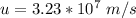Answer:
The value is
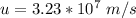
Step-by-step explanation:
From the question we are told that
The diameter of the nucleus is

The charge of the proton that makes up the nucleus is
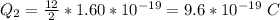
The energy to be impacted is
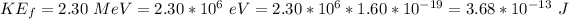
Generally the radius of the nucleus is mathematically represented as
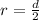
=>
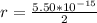
=>

Generally from the law energy conservation we have that
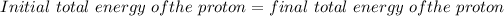
i.e
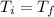
Here

Here
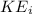 is the initial kinetic energy which is mathematically represented as
is the initial kinetic energy which is mathematically represented as
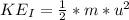
Here
 is the initial potential energy of the proton and the value is 0 J given that the proton is moving
is the initial potential energy of the proton and the value is 0 J given that the proton is moving
Also
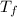 is mathematically represented as
is mathematically represented as
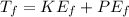
Here
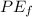 is the final potential energy which is mathematically represented as
is the final potential energy which is mathematically represented as
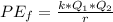
Here
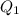 is the charge on the proton with a value of
is the charge on the proton with a value of
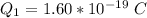
So
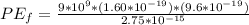
=>
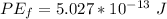
So
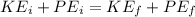
=>
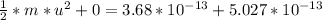
Here m is the mass of the moving proton with value

So
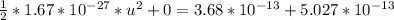
=>
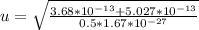
=>