Answer:
The smallest combination of the numbers is 20 and 140
Explanation:
The given parameters are;
The Highest Common Factor HCF of the two number = 20
The Lowest Common Multiple LCM of both numbers = Multiple of 14
Let x and y represent the two numbers, we are given;
x > y
We have;
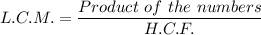
Substituting the known values, we have;
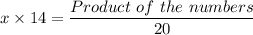
The product of the numbers = x × 14 × 20
The possible products of the numbers are;
280, 560, 840, 1,120, 1,400, 1,680, 1,960, 2,240, 2.520, 2,800, 3,080, 3,360, 3,640, 3,920
Dividing the possible products by 20 gives, the smallest quotient that is also a multiple of 20 as 140, from which we have;
20 × 140 = 2,800
Therefore, the smallest combination of the numbers = 20 and 140.