Question

-2x + 3y = 6

In the xy-plane, the graph of which of the following
equations is perpendicular to the graph of the
equation above?
A) 3x + 2y = 6
B) 3x + 4y = 6
C) 2x + 4y = 6
D) 2x + 6y = 3

Answer 1

The answer is A.

Explanation:

The perpendicular equation has a slope of the negative reciprocal. If we put the equation in slope-intercept form (y=mx+b), we can see the given equation's slope is 2/3. Therefore, the reciprocal must have a slope of -3/2 in slope intercept form (y= -3/2x+b).

Multiplying both sides of the equation by 2 to cancel the denominator, we have 2y = -3x +b. Then, move the -3 to the left side of the equation making the value positive, and we have 2y +3x = b. Therefore, A is the correct answer.

Answer 2

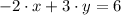`-2\cdot x + 3\cdot y = 6` is perpendicular to
`3\cdot x + 2\cdot y = 6`. (Answer: A)

Step-by-step explanation:

From Linear Algebra, we know that two vectors are perpendicular to each other when its Dot Product equals zero. In addition, a linear equation can be rewritten in this manner:

`a\cdot x + b\cdot y = c`

`(a, b)\, \bullet \, (x,y) = 0`

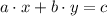
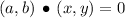
Where
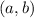`(a,b)` is the vector generator.

Then, if two lines are perpendicular to each other, then the dot product of respective vector generators must be zero. That is to say:

`(a, b) \, \bullet \, (c, d) = 0`

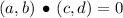
We proceed to check each case:

A)
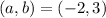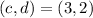
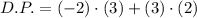
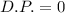
`(a, b) = (-2, 3)`,
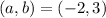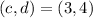
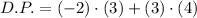
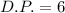
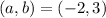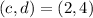
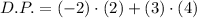
`(c, d) = (3, 2)`

`D.P. = (-2)\cdot (3) + (3)\cdot (2)`

`D.P. = 0`

B)
`(a, b) = (-2, 3)`,
`(c, d) = (3, 4)`

`D.P. = (-2)\cdot (3) + (3)\cdot (4)`

`D.P. = 6`

C)
`(a, b) = (-2, 3)`,
`(c, d) = (2, 4)`

`D.P. = (-2)\cdot (2) +(3)\cdot (4)`

`D.P. = 8`

D)
`(a, b) = (-2, 3)`,
`(c, d) = (2, 6)`

`D.P. = (-2)\cdot (2) + (3) \cdot (6)`

`D.P. = 14`

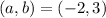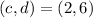
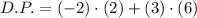
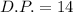
Which coincides with image attached below.

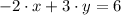`-2\cdot x + 3\cdot y = 6` is perpendicular to
`3\cdot x + 2\cdot y = 6`. (Answer: A)