Answer:
The final pressure of a gas is inversely proportional to the volume change and directly proportional to temperature
Step-by-step explanation:
Given
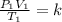
Required
Interpret
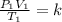
Multiply both sides by T1
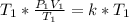
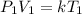
Divide both sides by V1
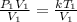
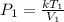
This can be rewritten as:
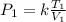
In the above expression; k is a constant of proportionality.
So, the equation can be written as variation as follows:
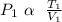
To interpret:
P varies directly to T (the numerator) and inversely to V (the denominator).