Answer:
the answer is A,
P(x) = -0.4x³+100x²-900x+500
Explanation:
monthly cost:
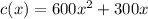
monthly revenue:
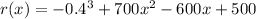
profit function:
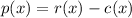

i) remove the first bracket
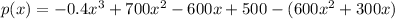
ii) there is a negative sign, '-' in front of the second bracket. so, change the sign of each term of the expression inside the bracket
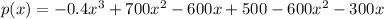
iii) collect like terms
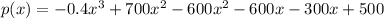
iv) simply the like terms
