Answer:
The correct option is C: 0.31 s.
Step-by-step explanation:
When the mass is then suddenly released we have:

Where:
F is the force
k: is the spring constant
Δy: is the spring displacement
Since the tension in the spring is zero, the force is the weight:
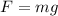
Where:
m is the mass of the object
g is the gravity
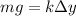 (1)
(1)
The oscillation period of the spring is given by:
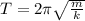 (2)
(2)
By solving equation (1) for "k" and entering into equation (2) we have:

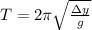
Since the spring will osclliates in a position between the initial position (when it is at rest) and the final position (when the mass is released and reaches the bottom), we have Δy = 2.5 cm = 0.025 m:
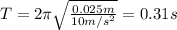
Hence, the oscillation period is 0.31 s.
The correct option is C: 0.31s.
I hope it helps you!